Page 19 - Ellingham, Mark, Mariusz Meszka, Primož Moravec, Enes Pasalic, 2014. 2014 PhD Summer School in Discrete Mathematics. Koper: University of Primorska Press. Famnit Lectures, 3.
P. 19
k Ellingham: Construction Techniques for Graph Embeddings 7
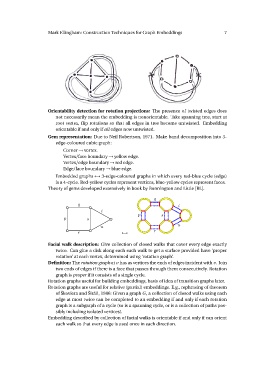
Orientability detection for rotation projections: The presence of twisted edges does
not necessarily mean the embedding is nonorientable. Take spanning tree, start at
root vertex, flip rotations so that all edges in tree become untwisted. Embedding
orientable if and only if all edges now untwisted.
Gem representation: Due to Neil Robertson, 1971. Make band decomposition into 3-
edge-coloured cubic graph:
Corner → vertex.
Vertex/face boundary → yellow edge.
Vertex/edge boundary → red edge.
Edge/face boundary → blue edge.
Embedded graphs ↔ 3-edge-coloured graphs in which every red-blue cycle (edge)
is a 4-cycle. Red-yellow cycles represent vertices, blue-yellow cycles represent faces.
Theory of gems developed extensively in book by Bonnington and Little [BL].
q p q t
t ↔ s u
ps r
u
r
Facial walk description: Give collection of closed walks that cover every edge exactly
twice. Can glue a disk along each such walk to get a surface provided have ‘proper
rotation’ at each vertex, determined using ‘rotation graph’.
Definition: The rotation graph at v has as vertices the ends of edges incident with v . Join
two ends of edges if there is a face that passes through them consecutively. Rotation
graph is proper if it consists of a single cycle.
Rotation graphs useful for building embeddings, basis of idea of transition graphs later.
Rotation graphs are useful for relative (partial) embeddings. E.g., rephrasing of theorem
of Škoviera and Širánˇ , 1986: Given a graph G , a collection of closed walks using each
edge at most twice can be completed to an embedding if and only if each rotation
graph is a subgraph of a cycle (so is a spanning cycle, or is a collection of paths pos-
sibly including isolated vertices).
Embedding described by collection of facial walks is orientable if and only if can orient
each walk so that every edge is used once in each direction.
Orientability detection for rotation projections: The presence of twisted edges does
not necessarily mean the embedding is nonorientable. Take spanning tree, start at
root vertex, flip rotations so that all edges in tree become untwisted. Embedding
orientable if and only if all edges now untwisted.
Gem representation: Due to Neil Robertson, 1971. Make band decomposition into 3-
edge-coloured cubic graph:
Corner → vertex.
Vertex/face boundary → yellow edge.
Vertex/edge boundary → red edge.
Edge/face boundary → blue edge.
Embedded graphs ↔ 3-edge-coloured graphs in which every red-blue cycle (edge)
is a 4-cycle. Red-yellow cycles represent vertices, blue-yellow cycles represent faces.
Theory of gems developed extensively in book by Bonnington and Little [BL].
q p q t
t ↔ s u
ps r
u
r
Facial walk description: Give collection of closed walks that cover every edge exactly
twice. Can glue a disk along each such walk to get a surface provided have ‘proper
rotation’ at each vertex, determined using ‘rotation graph’.
Definition: The rotation graph at v has as vertices the ends of edges incident with v . Join
two ends of edges if there is a face that passes through them consecutively. Rotation
graph is proper if it consists of a single cycle.
Rotation graphs useful for building embeddings, basis of idea of transition graphs later.
Rotation graphs are useful for relative (partial) embeddings. E.g., rephrasing of theorem
of Škoviera and Širánˇ , 1986: Given a graph G , a collection of closed walks using each
edge at most twice can be completed to an embedding if and only if each rotation
graph is a subgraph of a cycle (so is a spanning cycle, or is a collection of paths pos-
sibly including isolated vertices).
Embedding described by collection of facial walks is orientable if and only if can orient
each walk so that every edge is used once in each direction.