Page 34 - Ellingham, Mark, Mariusz Meszka, Primož Moravec, Enes Pasalic, 2014. 2014 PhD Summer School in Discrete Mathematics. Koper: University of Primorska Press. Famnit Lectures, 3.
P. 34
1.5 Transition graphs
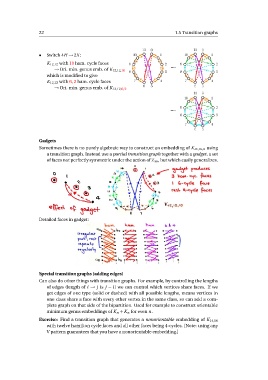
• Switch 4H → 2X : 11 0 11 0 1
10 1 10 2
3
K12,12 with 10 ham. cycle faces 9 2 0! 9
4
→ Ori. min. genus emb. of K12,12,10 8 38
which is modified to give 1
47 2
K12,12 with 6, 2 ham. cycle faces 7 65 3
→ Ori. min. genus emb. of K12,12,6/2 65 11 0 4
10
0! 9
8
7
65
Gadgets
Sometimes there is no purely algebraic way to construct an embedding of Km,m,n using
a transition graph. Instead use a partial transition graph together with a gadget, a set
of faces not perfectly symmetric under the action of m , but which easily generalizes.
Detailed faces in gadget:
Special transition graphs (adding edges)
Can also do other things with transition graphs. For example, by controlling the lengths
of edges (length of i → j is j − i ) we can control which vertices share faces. If we
get edges of one type (solid or dashed) with all possible lengths, means vertices in
one class share a face with every other vertex in the same class, so can add a com-
plete graph on that side of the bipartition. Used for example to construct orientable
minimum genus embeddings of Kn + Kn for even n .
Exercise: Find a transition graph that generates a nonorientable embedding of K14,14
with twelve hamilton cycle faces and all other faces being 4-cycles. [Note: using any
V pattern guarantees that you have a nonorientable embedding.]
• Switch 4H → 2X : 11 0 11 0 1
10 1 10 2
3
K12,12 with 10 ham. cycle faces 9 2 0! 9
4
→ Ori. min. genus emb. of K12,12,10 8 38
which is modified to give 1
47 2
K12,12 with 6, 2 ham. cycle faces 7 65 3
→ Ori. min. genus emb. of K12,12,6/2 65 11 0 4
10
0! 9
8
7
65
Gadgets
Sometimes there is no purely algebraic way to construct an embedding of Km,m,n using
a transition graph. Instead use a partial transition graph together with a gadget, a set
of faces not perfectly symmetric under the action of m , but which easily generalizes.
Detailed faces in gadget:
Special transition graphs (adding edges)
Can also do other things with transition graphs. For example, by controlling the lengths
of edges (length of i → j is j − i ) we can control which vertices share faces. If we
get edges of one type (solid or dashed) with all possible lengths, means vertices in
one class share a face with every other vertex in the same class, so can add a com-
plete graph on that side of the bipartition. Used for example to construct orientable
minimum genus embeddings of Kn + Kn for even n .
Exercise: Find a transition graph that generates a nonorientable embedding of K14,14
with twelve hamilton cycle faces and all other faces being 4-cycles. [Note: using any
V pattern guarantees that you have a nonorientable embedding.]