Page 214 - Leech, Jonathan E. 2020. Noncommutative Lattices: Skew Lattices, Skew Boolean Algebras and Beyond. Koper: University of Primorska Press
P. 214
Jonathan E. Leech │ Noncommutative Lattices: Skew Lattices, Skew Boolean Algebras and Beyond
I I
⎡1 0 0 0⎤ ⎡0 0 0 0⎤ ⎡1 0 0 0⎤ ⎡0 0 0 0⎤
⎢0 1 0 ∗⎥ ⎢∗ 1 0 0⎥ ⎢0 1 0 ∗⎥ ⎢∗ 1 0 0⎥
⎢ ⎥ ⎢ ⎥ ⎢0 ⎥ ⎢ ⎥
⎢⎣ 0 0 1 ∗ ⎦⎥ ⎣⎢ ∗ 0 1 0 ⎥⎦ ⎢⎣ 0 0 1 ∗ ⎥⎦ ⎢⎣ ∗ 0 1 0 ⎦⎥
0 0 0 0 0 0 0 1 0 0 0 0 0 0 1
⎡0 0 0 0⎤ ⎡0 0 0 0⎤
⎢∗ 1 0 ∗⎥ ⎢∗ 1 0 ∗⎥
(a) ⎢ ⎥ (b) ⎢ ⎥
⎢⎣ ∗ 0 1 ∗ ⎥⎦ ⎣⎢ ∗ 0 1 ∗ ⎦⎥
0 0 0 0 0 0 0 0
⎡0 0 0 0⎤ ⎡0 0 0 0⎤ ⎡0 0 0 0⎤
⎢∗ 1 0 ∗⎥ ⎢0 0 0 0⎥ ⎢∗ 1 ∗ ∗⎥
⎢ ⎥ ⎢ ⎥ ⎢0 0 0 0⎥
⎢⎣ 0 0 0 0 ⎥⎦ ⎣⎢ ∗ 0 1 ∗ ⎥⎦ ⎣⎢ 0 0 0 0 ⎦⎥
0 0 0 0 0 0 0 0
00
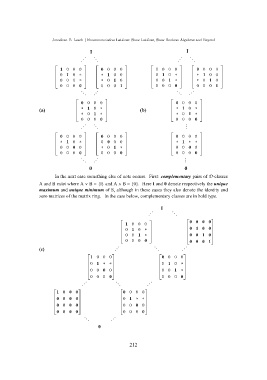
In the next case something else of note occurs. First: complementary pairs of D-classes
A and B exist where A ∨ B = {I} and A ∧ B = {0}. Here I and 0 denote respectively the unique
maximum and unique minimum of S, although in these cases they also denote the identity and
zero matrices of the matrix ring. In the case below, complementary classes are in bold type.
I
⎡1 0 0 0⎤ ⎡0 0 0 0⎤
⎢0 1 0 0⎥
⎢0 1 0 ∗⎥ ⎢⎢0 ⎥
⎢ ⎥ ⎥
⎢⎣ 0 0 1 ∗ ⎥⎦ 0 1 0
0 0 0 0
⎣⎢0 0 0 1⎥⎦
(c)
⎡1 0 0 0⎤ ⎡0 0 0 0⎤
⎢0 1 ∗ ∗⎥ ⎢0 1 0 ∗⎥
⎢⎢0 ⎥ ⎢⎢0 ⎥
0 0 0 ⎥ 0 1 ∗ ⎥
⎣⎢0 0 0 0⎥⎦ ⎣⎢0 0 0 0⎥⎦
⎡1 0 0 0⎤ ⎡0 0 0 0⎤
⎢0 0 0 0⎥ ⎢0 1 ∗ ∗⎥
⎢⎢0 0 0 0⎥⎥ ⎢⎢0 ⎥
⎣⎢0 0 0 0⎦⎥ 0 0 0 ⎥
⎣⎢0 0 0 0⎦⎥
0
212
I I
⎡1 0 0 0⎤ ⎡0 0 0 0⎤ ⎡1 0 0 0⎤ ⎡0 0 0 0⎤
⎢0 1 0 ∗⎥ ⎢∗ 1 0 0⎥ ⎢0 1 0 ∗⎥ ⎢∗ 1 0 0⎥
⎢ ⎥ ⎢ ⎥ ⎢0 ⎥ ⎢ ⎥
⎢⎣ 0 0 1 ∗ ⎦⎥ ⎣⎢ ∗ 0 1 0 ⎥⎦ ⎢⎣ 0 0 1 ∗ ⎥⎦ ⎢⎣ ∗ 0 1 0 ⎦⎥
0 0 0 0 0 0 0 1 0 0 0 0 0 0 1
⎡0 0 0 0⎤ ⎡0 0 0 0⎤
⎢∗ 1 0 ∗⎥ ⎢∗ 1 0 ∗⎥
(a) ⎢ ⎥ (b) ⎢ ⎥
⎢⎣ ∗ 0 1 ∗ ⎥⎦ ⎣⎢ ∗ 0 1 ∗ ⎦⎥
0 0 0 0 0 0 0 0
⎡0 0 0 0⎤ ⎡0 0 0 0⎤ ⎡0 0 0 0⎤
⎢∗ 1 0 ∗⎥ ⎢0 0 0 0⎥ ⎢∗ 1 ∗ ∗⎥
⎢ ⎥ ⎢ ⎥ ⎢0 0 0 0⎥
⎢⎣ 0 0 0 0 ⎥⎦ ⎣⎢ ∗ 0 1 ∗ ⎥⎦ ⎣⎢ 0 0 0 0 ⎦⎥
0 0 0 0 0 0 0 0
00
In the next case something else of note occurs. First: complementary pairs of D-classes
A and B exist where A ∨ B = {I} and A ∧ B = {0}. Here I and 0 denote respectively the unique
maximum and unique minimum of S, although in these cases they also denote the identity and
zero matrices of the matrix ring. In the case below, complementary classes are in bold type.
I
⎡1 0 0 0⎤ ⎡0 0 0 0⎤
⎢0 1 0 0⎥
⎢0 1 0 ∗⎥ ⎢⎢0 ⎥
⎢ ⎥ ⎥
⎢⎣ 0 0 1 ∗ ⎥⎦ 0 1 0
0 0 0 0
⎣⎢0 0 0 1⎥⎦
(c)
⎡1 0 0 0⎤ ⎡0 0 0 0⎤
⎢0 1 ∗ ∗⎥ ⎢0 1 0 ∗⎥
⎢⎢0 ⎥ ⎢⎢0 ⎥
0 0 0 ⎥ 0 1 ∗ ⎥
⎣⎢0 0 0 0⎥⎦ ⎣⎢0 0 0 0⎥⎦
⎡1 0 0 0⎤ ⎡0 0 0 0⎤
⎢0 0 0 0⎥ ⎢0 1 ∗ ∗⎥
⎢⎢0 0 0 0⎥⎥ ⎢⎢0 ⎥
⎣⎢0 0 0 0⎦⎥ 0 0 0 ⎥
⎣⎢0 0 0 0⎦⎥
0
212