Page 92 - Perdih, Andrej, Katja Lakota, Alja Prah. 2020. Strukture bioloških molekul. Univerzitetni učbenik z recenzijo in navodila za vaje. Koper: Založba Univerze na Primorskem.
P. 92
andrej perdih, katja lakota, alja prah
Pri metodi molekulske dinamike nove konformacije pridobimo z integriranjem klasičnih
Newtonovih enačb gibanja. Na nivoju atomov in molekul tako rešujemo II. Newtonov zakon, ki
ga za i-ti delec (atom) zapišemo kot:
!!""($) = &"($) = − ( )*+"($),
!$! '" '" )""($)
pri tem velja, da je sila Fi na i-ti delec (atom) z maso mi in ai pospešek delca i. Fi na i-ti delec je
enaka negativnemu gradientu potencialno energijske funkcije, ki je enaka produktu mase i-
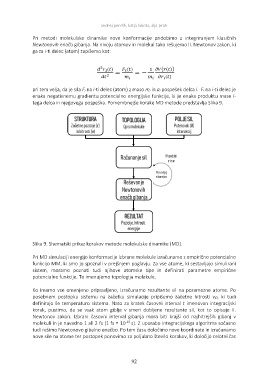
tega delca in njegovega pospeška. Pomembnejše korake MD metode predstavlja Slika 9.
Slika 9. Shematski prikaz korakov metode molekulske dinamike (MD).
Pri MD simulaciji energijo konformacije izbrane molekule izračunamo z empirično potencialno
funkcijo MM, ki smo jo spoznali v prejšnjem poglavju. Za vse atome, ki sestavljajo simulirani
sistem, moramo poznati tudi njihove atomske tipe in definirati parametre empirične
potencialne funkcije. To imenujemo topologija molekule.
Ko imamo vse omenjeno pripravljeno, izračunamo rezultante sil na posamezne atome. Po
posebnem postopku sistemu na začetku simulacije pripišemo začetne hitrosti vi0, ki tudi
definirajo še temperaturo sistema. Nato za kratek časovni interval t imenovan integracijski
korak, pustimo, da se vsak atom giblje v smeri dobljene rezultante sil, kot to opisuje II.
Newtonov zakon. Izbrani časovni interval gibanja mora biti krajši od najhitrejših gibanj v
molekuli in je navadno 1 ali 2 fs (1 fs = 10-15 s). Z uporabo integracijskega algoritma sočasno
tudi rešimo Newtonovo gibalno enačbo. Po tem času določimo nove koordinate in izračunamo
nove sile na atome ter postopek ponovimo za poljubno število korakov, ki določijo celotni čas
92
Pri metodi molekulske dinamike nove konformacije pridobimo z integriranjem klasičnih
Newtonovih enačb gibanja. Na nivoju atomov in molekul tako rešujemo II. Newtonov zakon, ki
ga za i-ti delec (atom) zapišemo kot:
!!""($) = &"($) = − ( )*+"($),
!$! '" '" )""($)
pri tem velja, da je sila Fi na i-ti delec (atom) z maso mi in ai pospešek delca i. Fi na i-ti delec je
enaka negativnemu gradientu potencialno energijske funkcije, ki je enaka produktu mase i-
tega delca in njegovega pospeška. Pomembnejše korake MD metode predstavlja Slika 9.
Slika 9. Shematski prikaz korakov metode molekulske dinamike (MD).
Pri MD simulaciji energijo konformacije izbrane molekule izračunamo z empirično potencialno
funkcijo MM, ki smo jo spoznali v prejšnjem poglavju. Za vse atome, ki sestavljajo simulirani
sistem, moramo poznati tudi njihove atomske tipe in definirati parametre empirične
potencialne funkcije. To imenujemo topologija molekule.
Ko imamo vse omenjeno pripravljeno, izračunamo rezultante sil na posamezne atome. Po
posebnem postopku sistemu na začetku simulacije pripišemo začetne hitrosti vi0, ki tudi
definirajo še temperaturo sistema. Nato za kratek časovni interval t imenovan integracijski
korak, pustimo, da se vsak atom giblje v smeri dobljene rezultante sil, kot to opisuje II.
Newtonov zakon. Izbrani časovni interval gibanja mora biti krajši od najhitrejših gibanj v
molekuli in je navadno 1 ali 2 fs (1 fs = 10-15 s). Z uporabo integracijskega algoritma sočasno
tudi rešimo Newtonovo gibalno enačbo. Po tem času določimo nove koordinate in izračunamo
nove sile na atome ter postopek ponovimo za poljubno število korakov, ki določijo celotni čas
92